Dynamic Programming
14 Aug 2020
Contents
What is Dynamic Programming
Dynamic Programming is simplifying a complicated problem by breaking it down into simpler broblems.
Dynamic Programming and Divide and Conquer
Dynamic programming and Divide and Conquer are similar but there are decisive differences. It is different whether repetition occurs or not in a small problem. Divide and Conquer is a way of dividing into just small problems to solve big problems and there is no repetition in small problems. However, dynamic programming uses the repetition of the answers of sub-problems.
In dynamic programming, all small problems must be solved only once. So, remember the answers to the small questions somewhere. Then, if the same small problem appears when we solve a bigger problem, use the answer to the small question that we remembered earlier.
Condition of Dynamic Programming
-
Small problems occur repeatedly. -
The same question has the same answer every time.
Dynamic programming can only be used if the above conditions are met.
Memoization
In dynamic programming, small questions are repeated and the answers to these small questions are always the same. Memoization means saving and reusing the correct answer to a small problem once calculated.
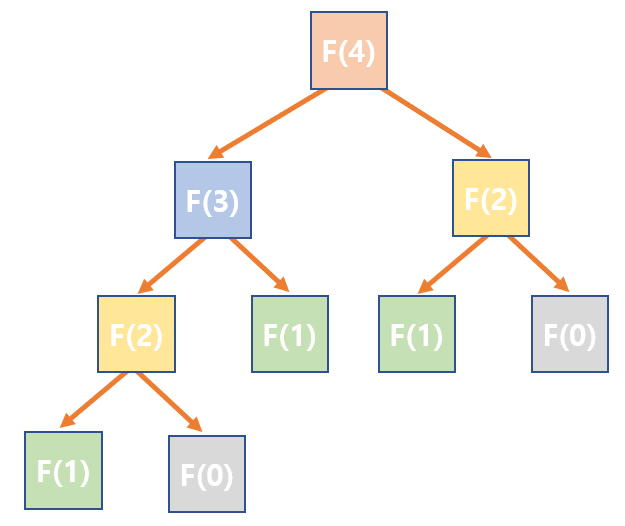
For example, Fibonacci sequence consist of numbers 1, 1, 2, 3, 5, 8.. and it means that Fib(n) = Fib(n-1) + Fib(n-2), for n > 1. This is simple to solve as a recursive function, but as n increases, the number of functions called increases exponentially.
In addition, there is a problem of having to do the previous work over and over again. At this time we can use dynamic programming to solve this problem.
1. Small problems occur repeatedly
For example, F(3) and F(2) are required to solve F(4). F(2) and F(1) are also required to solve F(3). Here we can see that F(2) is needed in duplicate.
2. The same question has the same answer every time
The values F(0) and F(1) in the Fibonacci sequence are always 0 and 1. Therefore, the value of F(2) is always 1. This is repeated over and over again.
def memoization_fibo(n):
# F(0) and F(1) are always 0 and 1.
memo[0] = 0
memo[1] = 1
if n < 2:
return memo[n]
for i in range(2, n+1):
# Fib(n) = Fib(n-1) + Fib(n-2)
# Store the values of the sequence in an array.
memo[i] = memo[i-1] + memo[i-2]
return memo[n]
if __name__ == '__main__':
n = 4
memo = [0 for i in range(n+2)]
print(memoization_fibo(n))
Bottom-up and Top-down
Bottom-up
Bottom-up uses loop. Bottom-up is a method of getting small problems one by one. It solves the sub-problems first and use their solutions to build-on and arrive at solutions to bigger sub-problems
def memoization_fibo_bottom_up(n):
memo[0] = 0
memo[1] = 1
if n < 2:
return memo[n]
for i in range(2, n+1):
memo[i] = memo[i-1] + memo[i-2]
return memo[n]
if __name__ == '__main__':
n = 4
memo = [0 for i in range(n+2)]
print(memoization_fibo_bottom_up(n))
Top-down
Top-down uses recursive function. If a small problem is not solved yet when we solve a big problem, then it starts to solve a small problem. Whenever we attempt to solve a new sub-problem, we first check if it is already solved.
def memoization_fibo_top_down(n):
if memo[n] > 0:
return memo[n]
if n < 2:
memo[n] = n
return memo[n]
else:
memo[n] = memoization_fibo_top_down(
n-1) + memoization_fibo_top_down(n-2)
return memo[n]
if __name__ == '__main__':
n = 4
memo = [0 for i in range(n+2)]
print(memoization_fibo_top_down(n))
The top-down method has the advantage of being easy to understand the ignition formula, and the Bottom-up method has the advantage of reducing time and memory usage because it does not use recursive function.