Dijkstra Algorithm
20 Aug 2020
Contents
What is Dijkstra Algorithm
Dijkstra Algorithm is an algorithm for finding the shortest paths between nodes in a graph.
Dijkstra Algorithm is the shortest path search algorithm that utilizes dynamic programming.
Time Complexity
- First, inspect all adjacent edges at each vertex.
- Second, push elements in the priority queue and delete them.
When you recall that each vertex is visited exactly once, and that all edges are inspected once, it takes a full O(|E|) time to inspect the edges.
The worst-case scenario with the largest priority queue is that each time all the edges in the graph are checked, the dist[] is updated and the number of vertices is added to the priority queue.
Because the addition occurs at most once for each edge, it can be seen that the number of elements added to the priority queue takes up to O(|E|) time, and that the overall time complexity is O(|E||log|E|) to do this for O(|E|) elements.
The time it takes for these two operations will result in O(|E|log|E|), but in most cases, the number of edges on the graph is less than |V|^2, so O(log|E|) = O(log|V|). Thus, the time complexity is O(|E|log|V|).
Conditions for Dijkstra Algorithm
Dijkstra Algorithmcan be used on graphs withnon-negativeedge weights.- Also, graph must be connected with edges.
But, the Bellman-Ford algorithm can be usd on graphs with negative edge weights.
Steps
- Mark all vertices as
unvisited. - Give all vertices a
tentativedistance value: set theinitial vertextozeroand all other vertices toinfinity. Set the initial vertex as thecurrent. - For the current vertex, consider all of its unvisited neighbors and calculate their tentative distances.
- After we are done considering all of the neighbors of the current vertex,
markthe current vertex asvisitedandremoveit from the unvisited set. A visited vertice will not be checked again. - If the destination vertex
has been marked visitedor if the smallest tentative distance among the nodes in the unvisited set isinfinity, then stop.[Finished] - Select the unvisited vertex that is marked with the smallest tentative distance, and set it as the new
current vertexthen go back to step 3.
Basic Example
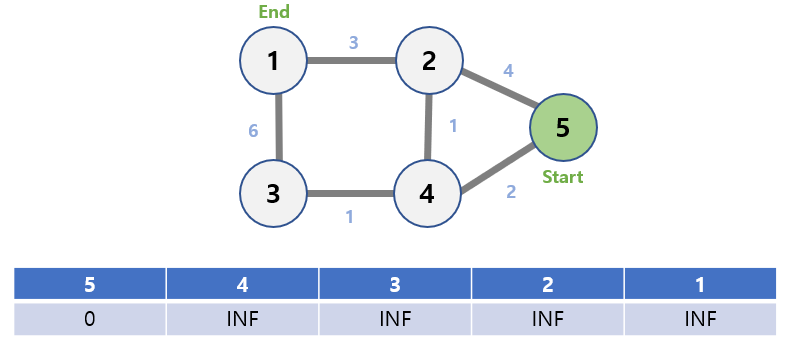
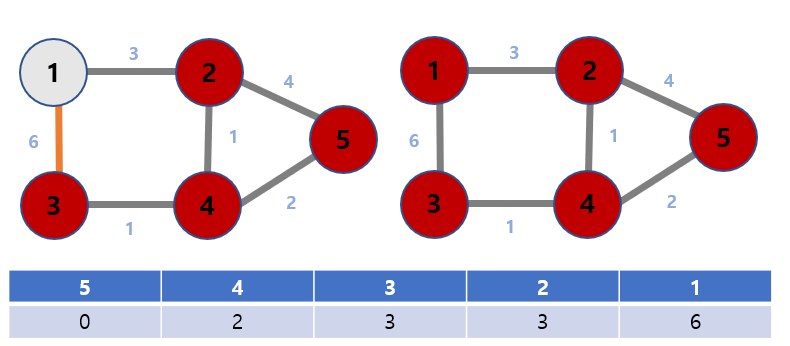
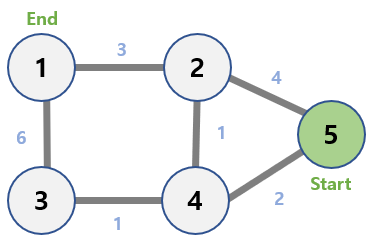
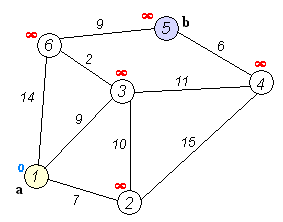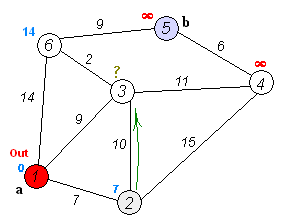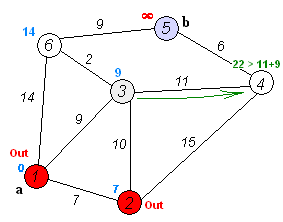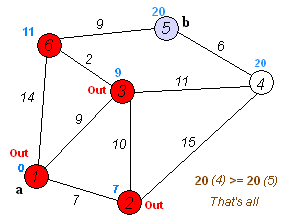
Let’s say we’re looking for the shortest path from vertex 5 to 1.
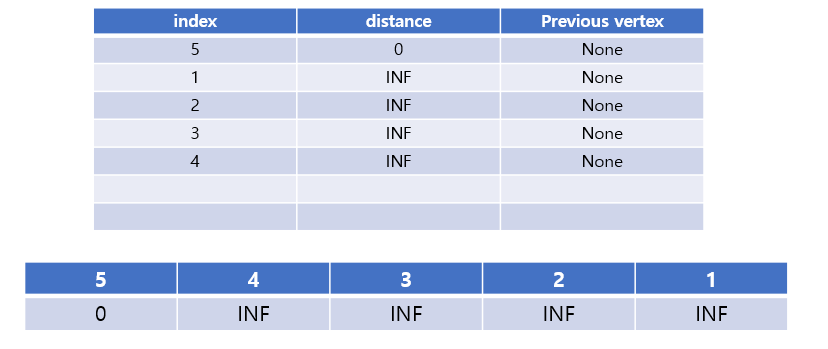
The shortest path of the remaining nodes, except for vertex number 5, becomes INF.
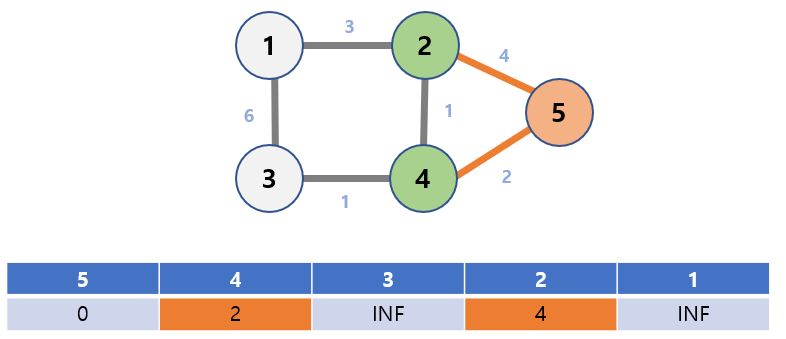
Nodes connected to node 5 are node 2 and node 4.
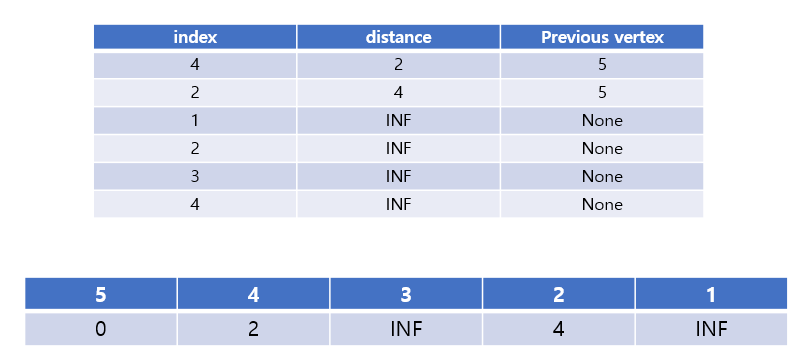
The shortest distance of node 2, dist[2] is min(dist[2], dist[5] + weight of 5 to 2) = min(INF, 0 + 4) = 4.
dist[4] = min(dist[4], dist[5] + weight of 5 to 4) = min(INF, 0 + 2) = 2.
Update the table values for nodes 2 and 4.
Now, Node 5 does not need to be visited.
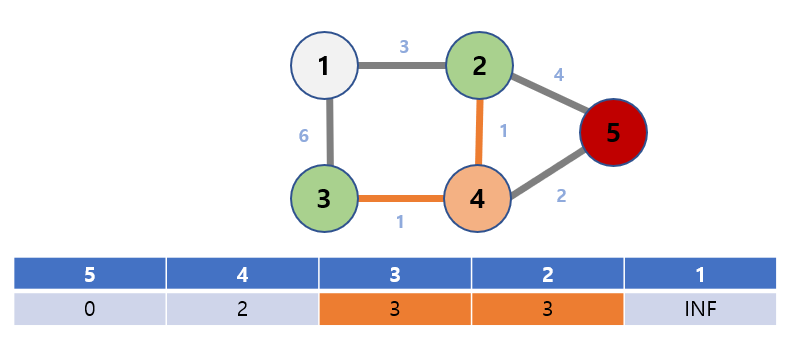
Next, we we look at node 4, which is the shortest distance from node 5.
Adjacent nodes of node 4 are node 2 and node 3.
dist[2] = min(dist[2], dist[4] + weight of 4 to 2) = min(2, 2 + 1) = 3.
dist[3] = min(dist[3], dist[4] + weight of 4 to 3) = min(2, 2 + 1) = 3.
Update the table values for nodes 2 and 3.
Now, Node 4 does not need to be visited.
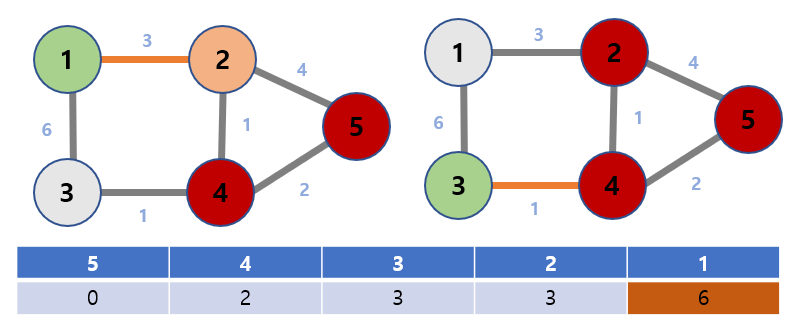
Because the shortest path values for nodes 2 and 3 are the same, check node 2 first.
The adjacent vertex of node 2 is node 1 and the weight is 3.
dist[1] = min(dist[1], dist[2] + weight of 2 to 1) = (INF, 3 + 3) = 6.
Update the table values for nodes 1.
Now, Node 2 does not need to be visited.
Next, check node 3.
The adjacent vertex of node 3 is node 1 and the weight is 6.
dist[1] = min(dist[1], dist[3] + weight of 3 to 1) = (6, 3 + 6) = 9.
However, the value of the new dist[1] = 9 is greater than the value of the existing dist[1] = 6, so there is no need to update the table.
Now, Node 1 does not need to be visited.
Therefore, the shortest path from vertex 5 to vertex 1 is 6.
Example with Priority Queue (Heap)
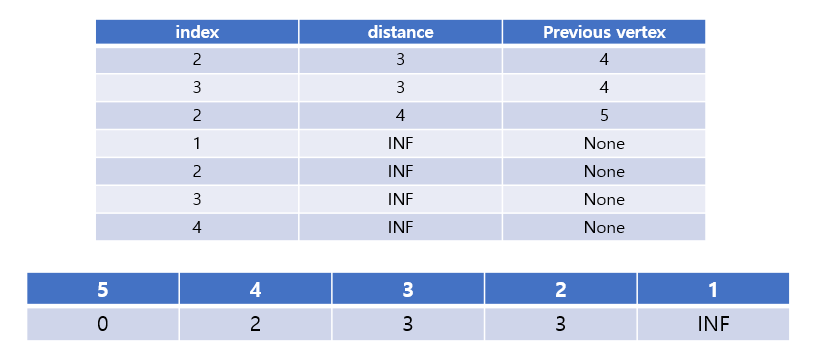
First, take the top value out of the heap with index of 5 and the distance of 0.
Compare the existing dist[5] with the distance.
Find adjacent nodes of 5 because both dist[5] and distance are equal to 0.
The vertices adjacent to node 5 are 2 and 4, with dist[2] = 4 and dist[4] = 2, respectively.
dist[2] = 4 < distance = INF and dist[4] = 2 < distance = INF, so push the values in the queue.
Take the top value out of the heap with index of 4 and the distance of 2.
Compare the existing dist[4] with the distance.
dist[4] = 2 = distance, so find adjacent nodes of 4.
The vertices adjacent to node 4 are 2 and 3, with dist[2] = 4 < INF and dist[3] = 3 < INF, respectively.
So, push the values in the queue.
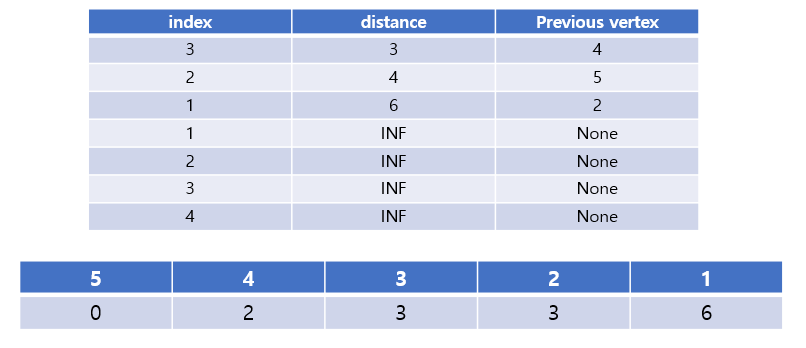
Take the top value out of the heap with index of 2 and the distance of 3.
Compare the existing dist[2] with the distance.
Find adjacent nodes of 2 because both dist[2] and distance are equal to 3.
The vertices adjacent to node 2 is node 1, with dist[1] = 6.
dist[1] = 6 < distance = INF, so push the value in the queue.
Take the top value out of the heap with index of 3 and the distance of 3.
Compare the existing dist[3] with the distance.
Find adjacent nodes of 3 because both dist[3] and distance are equal to 3.
The vertices adjacent to node 3 is node 1, with dist[1] = 9.
dist[1] = 9 > distance = 6, so pass it.
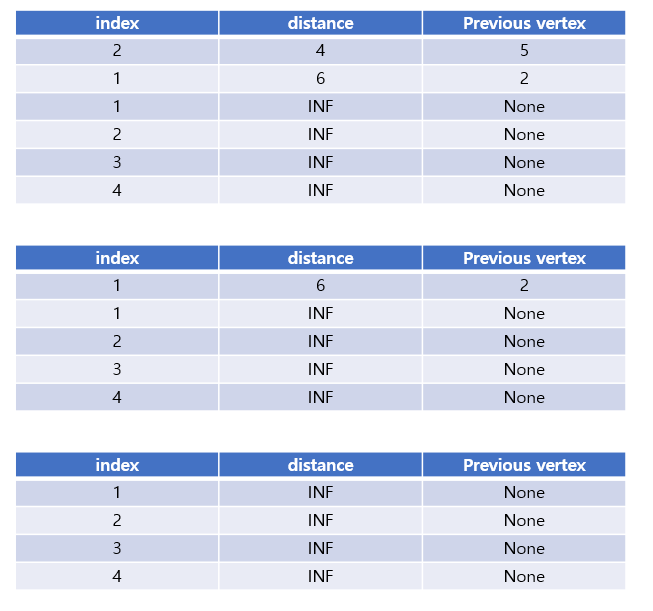
Take the top value out of the heap with index of 2 and the distance of 4.
Compare the existing dist[2] = 3 with the distance = 4.
dist[2] = 3 < distance = 4, so pass it.
Take the top value out of the heap with index of 1 and the distance of 6.
Just pass because the search for all vertices on the graph is over.
Now all existing dist[] values are less than INF, so there is no need to calculate.