What is Array Queue?

Contents

• What is Queue and How it works?
• Structure of Array List
  • Advantage of Array List
  • Disadvantage of Array List
• Operations for Array List
  • enqueue
  • dequeue
  • Peek
  • Implementation

What is Queue and How it works?

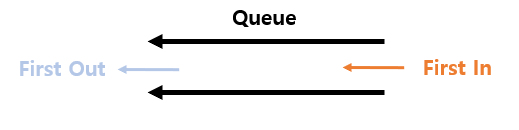
• Queue is a sequential structure that store data linearly.
• The order is FIFO(First In, First Out).
• When adding new data, add it to the rear location.
• When removing existing data, remove the data from the front location.
• Queue can be thought of as a horizontal structure.

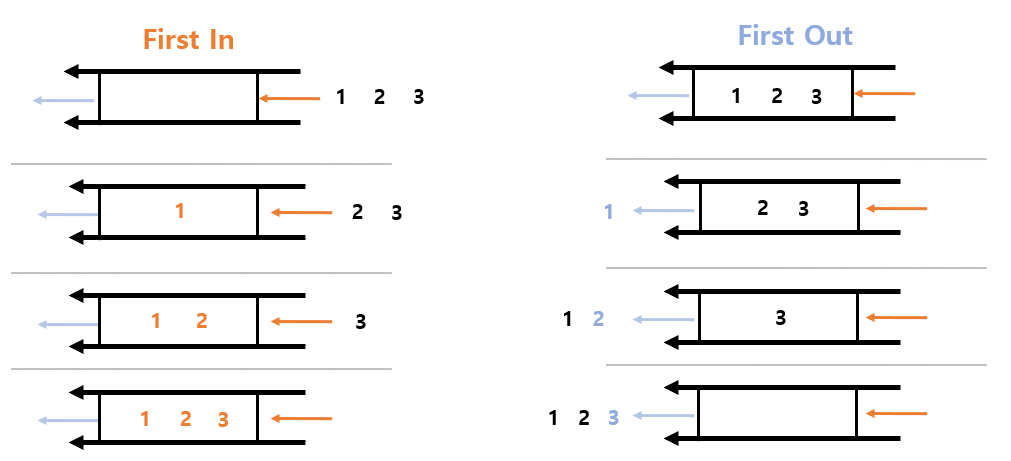
Structure of Array List

• Array Queue is implemented using array.
• Array Queue has front and rear.
  • The insertion of data occurs at front.
  • The deletion of data occurs at rear.

Advantage of Array List

• It takes O(1) to get the element in the array.

Disadvantage of Array List

• The size of the array is fixed, so you cannot insert more elements than the size of the array.
  • Resize is required when larger size array is needed.
• The empty space cannot be filled when the front moves ahead.

Operations for Array List

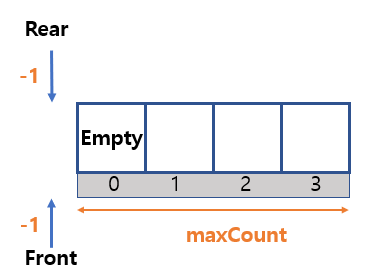
• First declare front and rear as -1.
  • rear = -1 means array is empty.

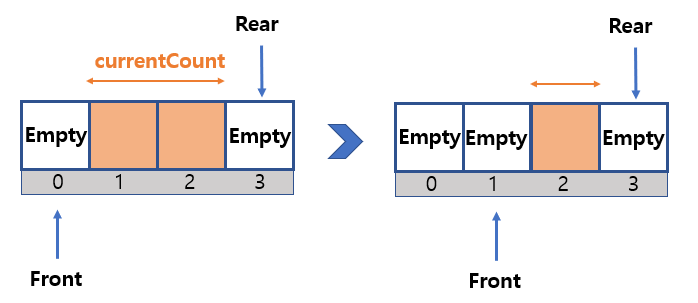
enqueue

• The location index of the last stored data in the array equals the value of the rear.
  • Therefore, when you add a new node, the location index of the node is rear + 1.
• If rear is equal to maxCount - 1, the queue is full.
  • maxCount is the maximum number of data that can be stored in an array.

// Change the position of rear.
queue->rear++;
// Add new Data in the array.
queue->pData[pQueue->rear].data = data;
// Increase current number of data.
queue->currentCount++;

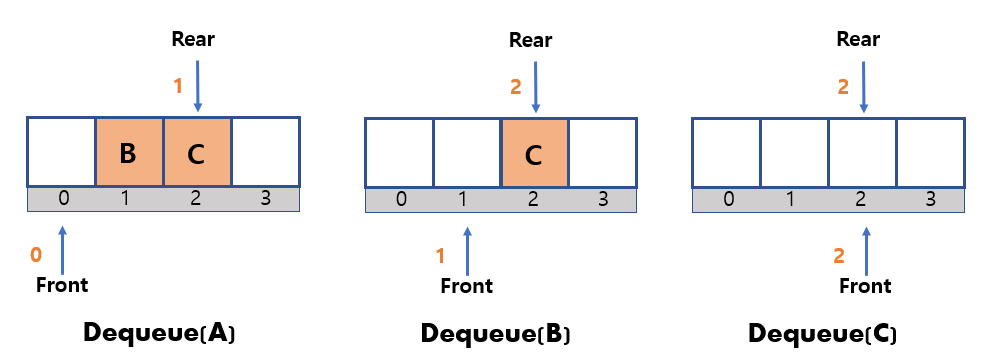
dequeue

• Remove the node on the front and return it.
• Then, incresase the front by 1.
• The value of the front is the value of the previous location index of the actual front node.
  • This is because the front was initially declared -1.
  • Also, this is important in the peek operation.

// Change the position of front.
queue->front++;

// Store the data of node to be removed.
pReturn->data = queue->pData[queue->front].data;

// Decrease current number of data.
queue->currentCount--;

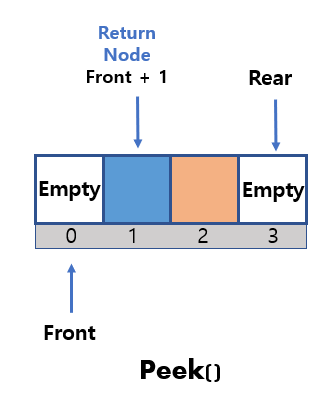
Peek

• Peek only returns the node in the front without removing it.
• Because the front was initially declared -1, the front + 1 location index must be used to return the data of the actual front node.

pReturn = &(queue->pData[queue->front + 1]);

Implementation

GitHub