Heap Implementation using Array

Contents

• Characteristic of using array for heap
• Position index and heap in an array
• Insertion of data in Max Heap
  • Basic principles
  • Process of insertion
• Deletion of data in Max Heap
  • Basic principles
  • Process of deletion
• Implementation

About Implementation of heap using array

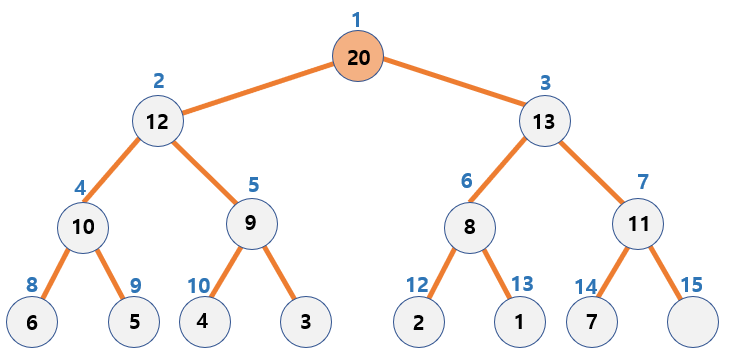
Characteristic of using array for heap

• Insertion and removal of the data is faster.
• We can calculate the address of a node, so we can quickly access the node we want.
• Because the heap is a complete binary tree, there are fewer empty nodes that are wasted, and thus less spaced is wasted.

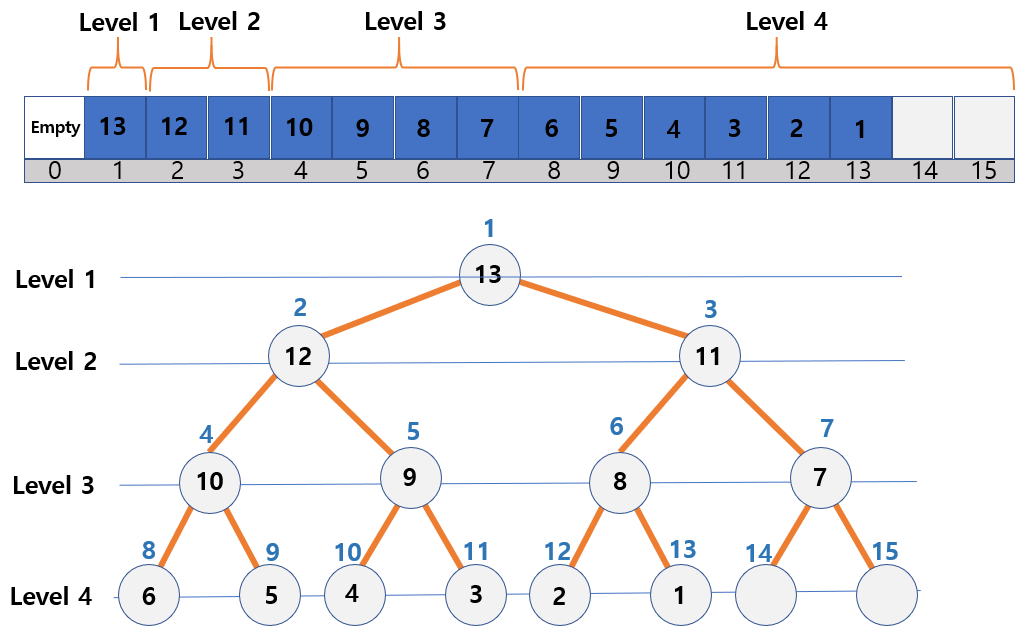
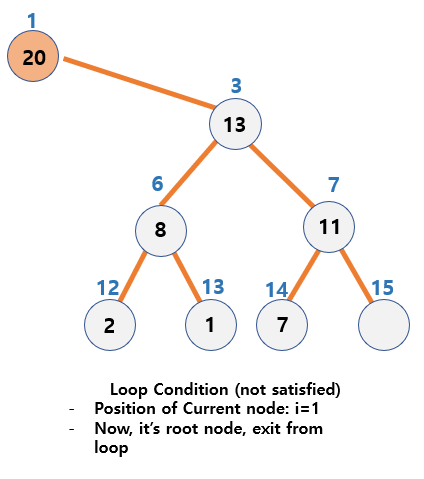
Position index and heap in an array

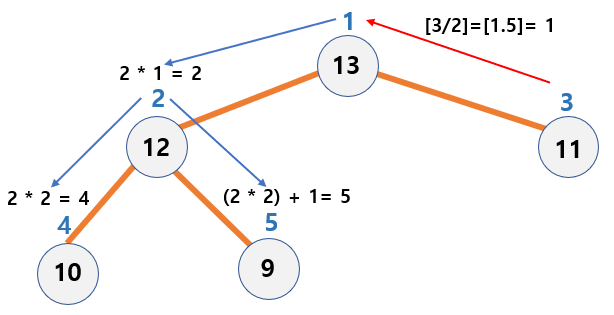
• The root node’s position index is 1.
• The parent node index of node i = [i / 2], if i > 1.
• Left child node’s index of node i = 2 * i
• Right child node’s index of node i = (2 * i) + 1

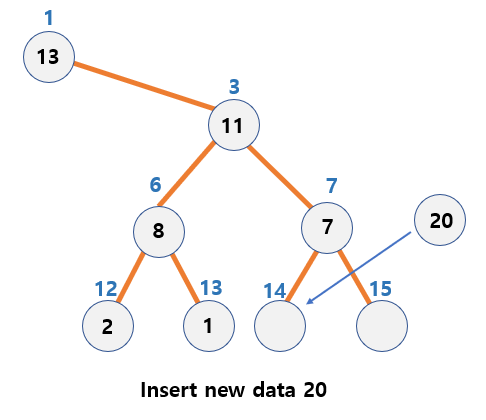
Insertion of data in Max Heap

Basic principles

1. Insert the new node next to the last node.
2. Move the position by comparing the value of the new node with the value of the parent node.

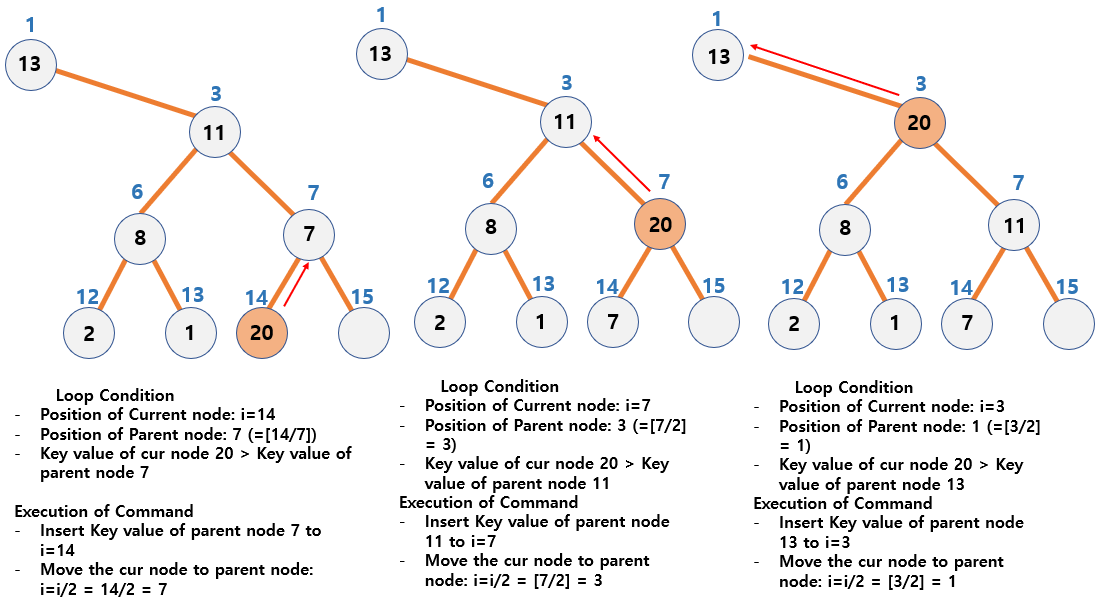
Process of insertion

1. i is set to the index pointing to the location of the last node of the heap

   • i = pHeap->currentCount

2. Set loop with conditions

   • if the current node location is not root
     • i != 1

   • if the value of the newly added data is greather than the value of the parent node`

     • value > pHeap->pData[i/2].data

3. Execution of command

   • Moves the value of the parent node to the current node’s position
     • pHeap->pData[i] = pHeap->pData[i/2]
   • Move the current node to the position of the parent node
     • i /= 2

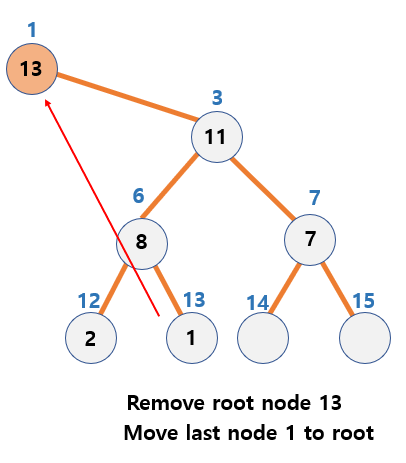
Deletion of data in Max Heap

Basic principles

1. Remove root node with maximum value
2. Insert the last node into the root node
3. Reconstruct the heap by moving nodes to meet the conditions of Max Heap

Process of deletion

1. Declare a variable

   • Point to the last node with pTemp
     • pTemp = &(pHeap->pData[pHeap->currentCount])
   • Declare parent = 1 to point to the root node, child = 2 to point the the left child node of the root node.

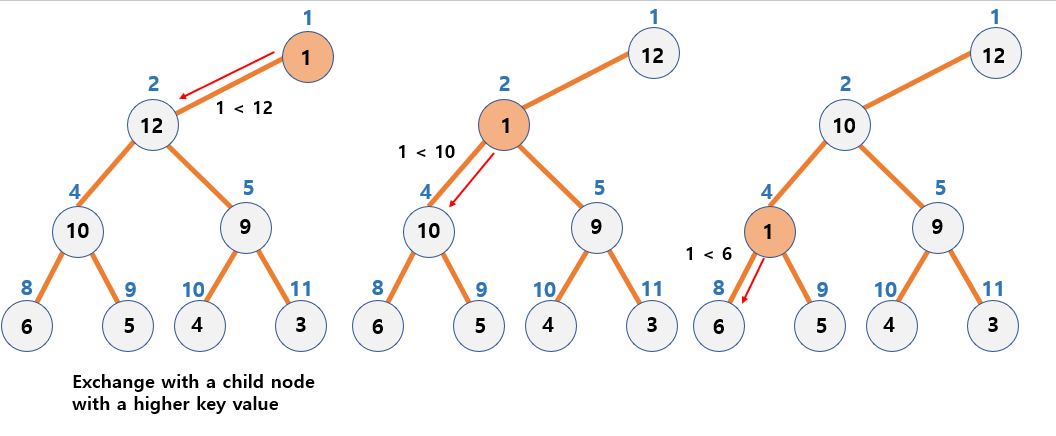
2. Set loop with conditions

   • Run the loop until the child variable meets the last node.
     • child <= pHeap->currentCount

3.Execution of command

• Compare the key values of the child nodes and move the nodes.
  • If the value of the right child node is greater than the value of the left child node to which the child variable points, modify the position index of the child variable.
  • pHeap->pData[child].data < pHeap->pData[child+1].data

Implementation

Github