What is a Graph and types of Graphs

Contents

• What is Graph?
• Difference between Tree and Graph
  • Characteristic of tree
  • Characteristic of graph
• Term of Graph
• Types of Graphs

About data structure Graph and its types

What is Graph?

• A graph is a set of nodes and edges.
  • G =(V,E)
• Graphs are non-linear data structures.

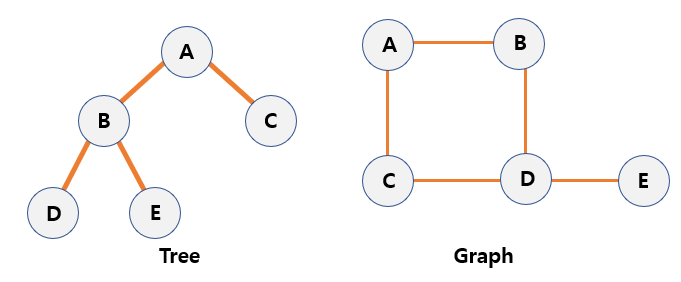
Difference between Tree and Graph

Characteristic of tree

• Root node exists
• The node except the root node is divided into subtrees.
• The tree extends downward.
• The tree must be connected.
• There is no loop.

Characteristic of graph

• The vertices on the graph can be connected to different vertices.
• You can set weights for the edge.
• Edges may or may not have direction.

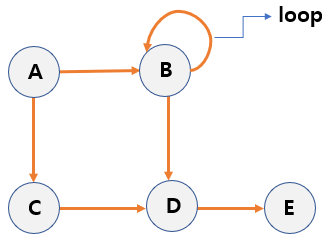
Term of Graph

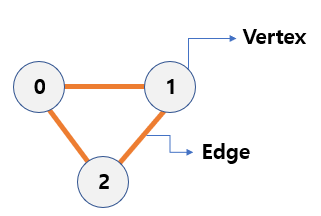
• Vertex - In the graph, each node represents a vertex.
• Edge - Edge means a line that connects two vertices.

• Adjacency - If two vertices are connected through a edge, the two vertices are adjacent.

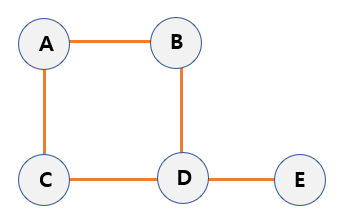
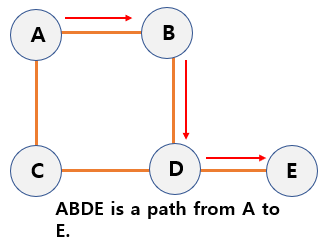
• Path - The path is the sequence of the edges connecting the two vertices.

  • Path length - The number of edges that consisting a path.
    • Path length of ABDE = 3
  • Simple path - If the nodes that consisting a path do not have the same node, it’s called a simple path.
  • Cycle - If the starting node and the last node of the path are the same, it is called a cycle.
  • Acyclic - Has no cycles.

  

• Degree - The number of edges connected to the vertex.
  • In Directed graph
    • In-degree - The number of edges entering the node.
    • Out-degree - The number of edges leaving the node.
• Loop - When there is a edge from a node to itself, it’s called a loop.

Types of Graphs

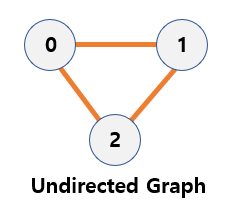
• Undirected graph
  • Graph witout directoin on the edges connecting nodes.
  • We can move the two nodes in both directions.
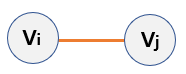
  • The edge can be expressed in (Vi,Vj) or (Vj,Vi).

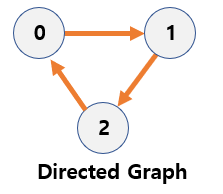
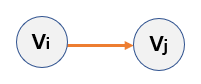
• Directed graph

  • Graph with direction on the edges connecting nodes
  • It is only possible to move in a specific direction on both nodes.
  • The edge can be expressed in (Vi,Vj).

  

  

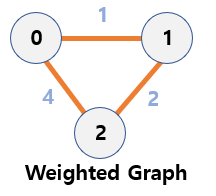
• Weighted graph

  • A graph with weights on the edges connecting nodes.
  • It is also called a network.

  

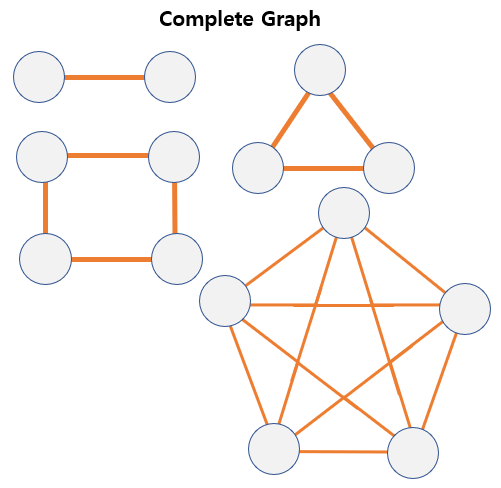
• Complete graph

  • A graph in which all vertices on a graph are connected 1:1.
  • All nodes are connected to each other, so there is no edge to add.

  • It has the maximum number of connectable edges.

    • Max number of edges
    • Undirected graph: n(n-1) / 2, n = number of nodes.
    • Directed graph: n(n-1)

    

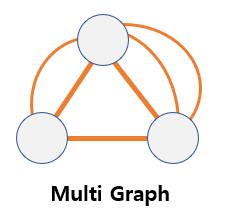
• Multi graph

  • Several edges are connected between the two vertices.

  

• Sub-graph

  • A graph created by excluding some edges from the original graph.
  • A graph whose vertices and edges are subsets of original graph.
  • G2 is a sub-graph of G1.

  

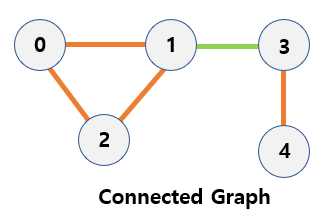
• Connected graph

  • A graph in which it’s possible to get from every vertex to every other vertex through edges.

  

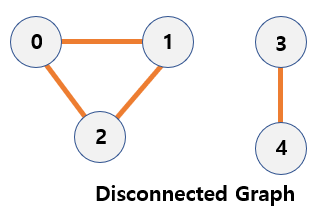
• Disconnected graph

  • If at least two vertices of the graph are not connected by a edge, it is a disconnected graph.