How to implement Graph

Contents

• Abstract data type of Graph
• Implementation method of Graph
  • 1. Adjancency Matrix
  • 2. Adjancency List
• Implementation

About Data Structure Graph Implementation Method

Abstract data type of Graph

• Create Graph - Creates an empty graph with n nodes.
• Delete Graph - Remove all nodes V and edges E of Graph G, then remove the graph.
• Add Edge - Add an edge that connects node u and v of Graph G
• Delete Edge - Remove an edge (u,v) or (v,u) of Graph G

If a graph is Directed Graph, u->v and v->u are different edges.

Implementation method of Graph

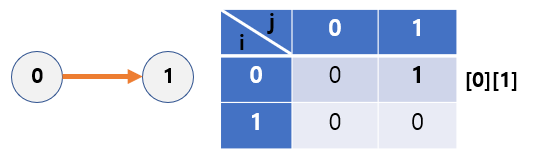
1. Adjancency Matrix

• Use a two-dimensional array (aka matrix)
• Adjacent if two nodes are connected by an edge.
• Store information about the edge of the graph in adhacent matrix.
• The existence of an edge
  • If an edge (i,j) exists: [i][j] = 1
  • If an edge (i,j) does not exists: [i][j] = 0

Advantage of Adjacent Matrix

• It is fast to check the edge information of two nodes. O(1)
• It is fast to add and remove new edges. O(1)

Problems with Adjacent Matrix

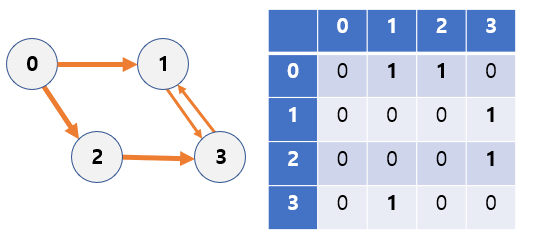
1. Regardless of the number of edges, the size of the array is always N*N (N is the number of nodes).
   • Because the above graph has four nodes, the number of elemnts in the array (4*4) = 24.
   • Use memory as much as O(N^2).
2. All nodes must be traversed in order to find a node adjacent to a particular node.
3. O(N^2) to add or remove nodes.
4. O(N^2) to find the number of all edges in the graph.

Adjacent matrix is better used when the number of nodes is relatively small and the number of edges is high. Therefore, it is suitable for Dense Graph, which has many edges.

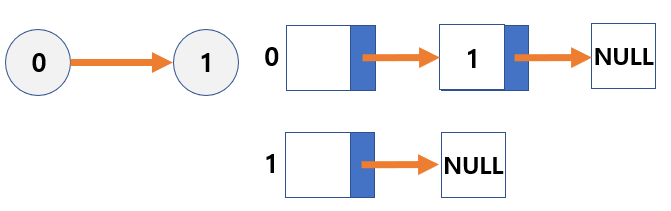
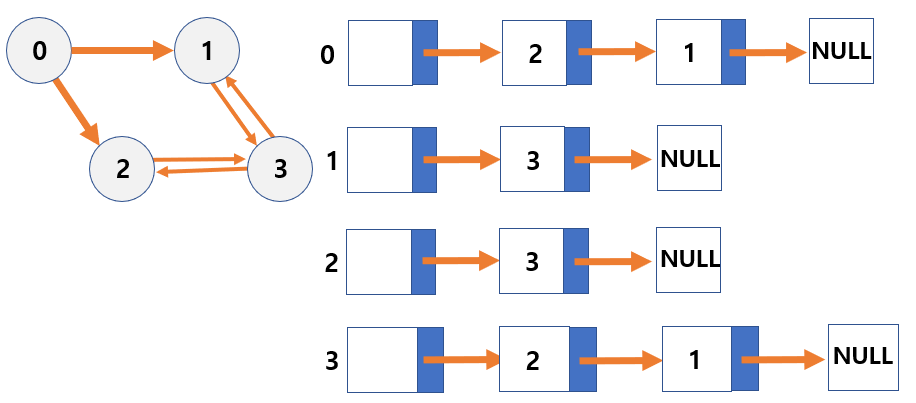
2. Adjancency List

• List fro storing adjacent information
• A one-dimensional array of linked list.
  • The linked list is stored in a one-dimensional array by the number of nodes from the root node in the graph.
• The size of the array equals the number of nodes in the graph.

Advantage of Adjacent List

1. Memory efficiency is good.
2. Memory usage depends on the number of edges, not the number of nodes.
3. It has direct access to a specific node, making it easy to find adjacent nodes.
4. It is fast to add and remove nodes.
5. It is fast to add edges. O(1)
6. O(N+E) to find the number of all edges in the graph.

Problems with Adjacent Matrix

1. It takes a long time to check the edge information of the two nodes.

Adjacent list is better used when the number of nodes is large and the number of edges is relatively small. Therefore, it is suitable for Sparse graph, which has less edges.

Implementation

Adjacency List and Adjacency Matrix GitHub